4.        Stabilita koryta

4.1        Kritické tečné napětí

Pohyb splavenin je určen poměrem sil uvádějících zrna splavenin do pohybu a sil bránících tomuto pohybu.

Síly způsobující pohyb zrn:

a)      smyková síla vyvolaná proudící vodou, působící na povrchu zrna splavenin

b)      tečná složka tíhy zrna-leží-li zrno splavenin na nakloněné rovině

c)      vztlaková hydrodynamická síla

            t - tečné napětí (Pa)

            d - průměr zrna splavenin (m)

            C₁, C₂ - opravný součinitel objemu částic a plochy průmětu částice do horizontální          roviny

            g - gravitační zrychlení (m.s^-2)

            r_s, r - hustota splavenin a vody (kg.m^-3)

            a - úhel odklonu dané plochy od vodorovné roviny (°)

            u - rychlost proudění v blízkosti uvažované částice (dnová rychlost) (m.s^-1)

C_L - součinitel zdvihové síly

Síly bránící pohybu zrn:

a)      vlastní tíha částice pod vodou

b)      síla tření daná tíhou částice

Další síly, které nelze exaktně určit (síly vyplývající z):

• vazeb mezi zrny
• vyplnění pórů štěrkopískových směsí jemnými částicemi
• tvarové nepravidelnosti.

Počátek pohybu splavenin je jev nahodilý v čase i prostoru, určení je velmi obtížné.

Rozlišujeme tři fáze pohybu splavenin:

1. počáteční pohyb - pohybují se jednotlivá zrna, max. tolik, že je možno určit počet na plošné jednotce. Pohybují se zrna malých průměrů vůči ostatním.
2. Střední pohyb - pohyb zrn středních velikostí. Je jich takové množství, že nelze stanovit počet zrn na plošné jednotce, pohyb splavenin má, ale místní charakter, nenastávají významnější deformace dna.
3. Všeobecný pohyb splavenin - nastává pohyb i největších zrn. zrna se pohybují v souvislém proudu.

Při úpravách toků se nejčastěji hledá takové tečné napětí na dně koryta toku, při kterém začíná pohyb splavenin. Toto napětí je obvykle označováno jako kritické tečné (tangenciální) napětí. Dojde-li k překročení této hodnoty nastává pohyb splavenin. Nejčastěji se stanovuje kritické tečné napětí pro danou velikost zrna pomocí Shieldsových grafů.

• Shields ukázal funkční závislost kritického tečného napětí na režimu proudění (závislost na Re_d)
• Na obr. 3.24 je zobrazena závislost mezi Shieldsovým parametrem a Re_d
• Jsou na něm vyznačeny oblasti tvorby dnových útvarů a poměr mezi tloušťkou laminární podvrstvy a velikosti průměru zrn splavenin

I.        oblast              d>d

• max. hodnota Shieldsova parametru je 0,6
• platí pro zrna hranatá a stejného průměru
• mezní hodnota této oblasti je dána vztahem

oblast ohraničuje       

II.        druhá přechodná oblast          d=d

• je ohraničena Re_d=10
• nejmenší hodnota Shieldsova parametru 0,03

III.      třetí přechodná oblast            d<d

• je ohraničena Re_d=10³
• hodnota Shieldsova parametru 0,06
• turbulantní proudění není ještě zcela vyvinuté, závislost na Re_d platí

IV.             oblast

• křivka přechází do rovnoběžky s vodorovnou osou
• jedná se o oblast turbulentního proudění
• Shieldsův parametr přestává být závislý na Re

4.2        Nevymílací rychlost

• je adekvátní termín ke kritickému tečnému napětí
• jde o rychlost proudění v okamžiku, kdy existuje rovnováha sil způsobujících pohyb splavenin a sil, které tomuto pohybu brání
• je definována jako mezní rychlost, jejíž překročení způsobuje pohyb splavenin
• dnová-místní rychlost u dna se stanoví jako mezní rychlost
• svislicová-určí se za mezní odpovídající svislicová rychlost
• průřezová-určená pro mezní stav splavenin, kdy začíná jejich pohyb

Nevymílací rychlost se teoreticky stanoví stejně jako kritické tečné napětí.

Na zrno splavenin ležící na dně toku působí síly:

• tečná složka tíhy
• vztlaková hydrodynamická síla
• hydrodynamická tlaková síla

  

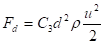
• síla tření

Výsledná podmínka rovnováhy sil po matematické úpravě

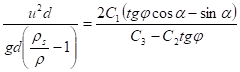
            u - dnová rychlost (nevymílací)

C₁, C₂, C₃-součinitele zahrnující tvarové odlišnosti zrn od geometrických tvarů.

V praxi i v literatuře se u nás nejčastěji objevují následující vztahy:

Šamova          

Gončarova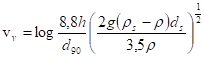     

Meyer-Petera            (kN.m³)

J.J. Leviho

Pro 10<h/d_s<60      

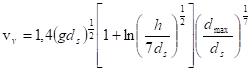
Pro h/d_s>60    

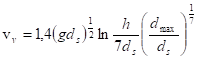
Mavise pro nevymílací dnovou rychlost

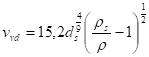
4.3        Průtok splavenin

• při pohybu splavenin jsou unášena zrna v povrchové vrstvě dna přibližně o síle dvou průměrů zrn splavenin
• z obr. 3.26 je patrné, že dnová rychlost ovlivňuje pohyb splavenin v povrchové vrstvě dna
• pod pohybující se vrstvou zrna splavenin setrvávají v klidu-vytvářejí pevné dno
• formy pohybu splavenin
  • valení
  • sunutí
  • poskoky
  • pohyb v souvislé vrstvě ve směru proudění-závisí na rychlosti
  • malá zrna unášena ve formě suspenze
• plaveniny jsou suspendované splaveniny
  • průtok = pevné částice/objem kapaliny
• průtok splavenin určíme v daném profilu při daném průtoku vody:
  • z hydraulických parametrů a původních vlastností aluviálního materiálu koryta
  • jako přítok z horního úseku nad sledovaným profilem.

Průtok splavenin a plavenin, jejich unášení proudem a jejich ukládání je závislé na celé řadě faktorů:

1.      veličiny ovlivňující odnos splavenin

Velikost zrn, sedimentační rychlost, hustota, tvar zrn, odpor vůči obrusu, koheze; geologie a topografie povodí; atmosférické srážky-velikost, intenzita, doba trvání, rozdělení v jednotlivých ročních obdobích; půdní podmínky, vegetační kryt, kultivace pozemků, pastva, povrchová eroze; vymílání břehů.

2.      veličiny ovlivňující množství odnášených splavenin

Geometrické vlastnosti a tvar přímého proudění-hloubka, šířka, tvar a napřímení; hydraulické vlastnosti říčního koryta-sklon, drsnost, hydraulický poloměr, průtok, rychlost, rozdělení rychlosti, turbulence, tečné napětí, vlastnosti kapaliny, rovnoměrnost průtoku.

Některé z uvedených veličin je obtížné analyzovat a kvantifikovat. Je třeba provádět dlouhodobá měření a pozorování veličin a stanovit jejich zákonitou proměnlivost.

Nejčastěji jsou pro praktické použití doporučovány dvě metody:

Einstein-Brownova

a)      stanovení časového faktoru

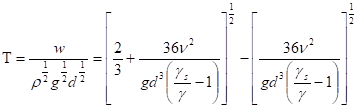
b)      průtok splavenin je obsažen v tzv. Einsteinově parametru

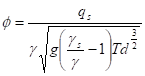
c)      parametr f je funkcí parametru intenzity proudění

Průtok splavenin po výpočtu veličin y se určí pomocí grafů na obr. 9 a 10.

Meyer-Peterova

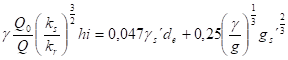
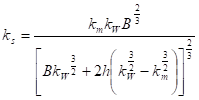
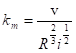
k_W - drsnost stěn

Q₀ - průtok příslušný té části koryta, ve které existuje pohyb splavenin

Q - celkový průtok korytem

q_s´ - průtok splavenin na šířce 1m za 1s

B - šířka koryta ve dně

4.4        Průtok plavenin

• plaveniny se do toku dostávají:
  • erozí dna a svahů říčního koryta
  • obrusem splavenin
  • splachem z povrchu okolního území
  • umělými zásahy do toku-výstavba objektů, zaústění kanalizace
• zakalují tok
• rozptýlením částic v kapalině vzniká směs kapaliny a pevných látek - dispersoid
• tam kde poklesnou rychlosti proudění dojde k sedimentaci plavenin - důležité u nádrží
• množství plavenin se udává

a)      jako koncentrace pevných látek, tj. množství pevných látek v objemové jednotce

b)      jako průtok plavenin v daném příčném profilu za jednotku času

• velikost plavenin je různá
• jejich koncentrace (průtok) je ovlivňován právě velikostí zrn plavenin, z toho vyplývá nutnost znát granulometrické složení plavenin
• průtok se pak vyjadřuje jako součet průtoků různých frakcí plavenin
• jejich percentuální obsah z daného celkového množství

    (%)

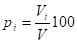  V_i - objem i-té frakce celkového objemu V

• průtok plavenin na 1m šířky - měrný průtok.

4.5        Stabilita koryta upraveného toku

Stabilita - schopnost koryta toku zachovávat hloubku a tvar příčného profilu i směr.

Odolnost - schopnost koryta toku odolávat účinkům proudící vody v korytě, vln, chodu ledů apod.

Oba pojmy jsou významově blízké. Stabilita koryta znamená stálost poměrů nebo rovnováhu mezi silami, které namáhají říční koryto a silami, které působí proti těmto silám.

Stabilita

• neproměnnost koryta při proudění vody i při suchém korytě
• stabilita svahu v suchém stavu, nedochází k erozi při proudění ani se nezanáší splaveninami
• neproměnnost trasy toku.

4.6        Způsoby posouzení stability říčního koryta

Stabilitu koryta v suchém stavu posuzují metody mechaniky zemin.

Namáhání říčního koryta prouděním vody se posuzuje:

a)      metoda průřezové rychlosti

• nejčastěji je při posuzování stability říčního koryta používána nevymílací rychlost a nezanášecí rychlost
• obecně musí být splněna nerovnost

  v_n < v < v_v

  v_n - nezanášecí rychlost

  v - průřezová rychlost

  v_v - nevymílací rychlost

  v_n = 0,7 v_v

b)      metoda svislicové rychlosti

• zahrnuje změny velikosti svislicových rychlostí po šířce koryta
• požaduje se splnění nerovnosti

  v_sn < v_smax < v_sv

• je obtížné najít ke svislicové rychlosti adekvátní nevymílací svislicovou rychlost v_sv a nezanášecí rychlost
• lze použít vztah 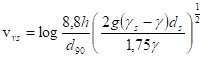, u širokých koryt  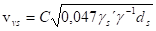a ostatní vztahy pro průřezovou nevymílací rychlost pokud R@h
• v_sn=0,7v_sv

c)      metoda dnové rychlosti

• stav říčního dna je možné posoudit pomocí místní dnové rychlosti u_d
• vznikají stejné problémy jako u svislicové rychlosti
• dnovou rychlost lze určit ze vztahu

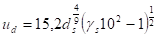
d)     metoda tečného napětí

• tečné napětí působící po omočeném obvodu říčního koryta způsobuje deformace říčního koryta
• platí podmínka t<t_k nemá-li dojít k erozi
• pomocí tečného napětí nelze stanovit zda dojde k sedimentaci splavenin

e)      metoda stupně bezpečnosti

• u nás se nepoužívá, uvádí se v anglosaské literatuře

  

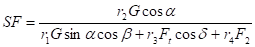
• význam symbolů viz obr. 3.36
• nepůsobí-li proudění vody, platí b=0, l=0, a=j a SF=1
• číslo stability částic ležících na nakloněné rovině

  

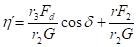
• pro částice ležící na rovném dně a=0, d=0

                      

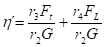
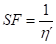
• pro začátek pohybu splavenin při proudění na rovném dně bude SF=1 a h´=1
• na nakloněné rovině při působení proudění vody SF=1 znamená stabilitu svahu v uvažovaném místě.

Posuzování stability říčního koryta může být prováděno pro řadu průtoků. Zdá se logické požadovat stabilitu pro max. průtoky. Z ekonomického hlediska by však užitek dosažený úpravou byl neúměrně drahý.

Norma ČSN 736820 doporučuje následující průtoky pro posouzení stability jednotlivých částí říčního koryta:

• pro neopevněný břeh a bermu koryta průtoky    Q₅ - Q₂₀
• pro opevněný břeh a bermu                                 Q₂₀ - Q₁₀₀
• pro dno toku                                                        Q₁ - Q₅ - jedná se o relativně nízké průtoky, protože prohloubení dna při vyšších průtocích se nerozšíří pod patky břehových opevnění Þ základová spára patky musí ležet pod očekávaným prohloubením nebo musí být její objem tak velký, že by při postupném sesouvání kamene vyplnil vznikající výmol.

4.7        Stabilita říčního koryta v přímé trati

Musíme rozlišit části omočeného obvodu podle sklonitosti:

• pro dno musí být splněny nerovnosti uvedené v předchozí kapitole, má-li dno zůstat stabilní při zvoleném návrhovém průtoku
• při posuzování odolnosti svahu ovlivní stabilitu této části koryta sklon daný úhlem a.

Stabilita svahu je dána rovnováhou složek působících sil v rovině svahu.

Na částice působí hlavně tyto síly:

• tíha částice G
• smyková síla F_t
• síla tření F
• hydrodynamická vztlaková síla F_L-působí opačně než síla tíže, zmenšuje účinek síly tíže částice

výsledná síla působící ve směru tíže je          G´=G-F_L

tečná složka tíhy je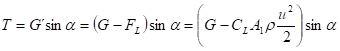    

normálová složka tíhy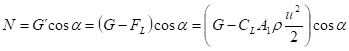

            F_L - lze obtížně vyjádřit

            U - rychlost v rovině svahu břehu

C_L - součinitel tvaru

A₁ - průmět částice do roviny kolmé k proudění

Hydrodynamická síla se kvůli uvedeným problémům zanedbává.

Podmínka rovnováhy má pak tvar

při rovném stabilním dně platí

h_d - hloubka při průtoku, při němž je dno stabilní.

Hloubka h_d se určí ze souřadnic průsečíků průběhů funkcí h = f (v) a h = f (v_v).

Při dosazení vztahu pro stabilní rovné dno do rovnice pro podmínku rovnováhy se po úpravě získá:

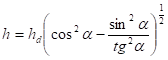
Hloubka h na svahu označuje mez kdy jsou síly působící na částici v rovnováze a nedochází k deformaci. Bylo zanedbáno: vliv uložení zrn, ulehlost zemin, F_L, koheze.

V praxi se používá ke stanovení výšky opevnění

h < vypočítaná hodnota Þ svah břehu je stabilní

h > vypočítaná hodnota Þ svah břehu je nestabilní

Při použití nevymílacích rychlostí

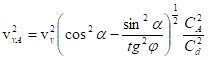
v_vA - nevymílací rychlost v daném bodě A na svahu koryta

v_v - nevymílací rychlost pro dno

C_A - Chézyho rychlostní součinitel v bodě A

C_d - Chézyho rychlostní součinitel pro dno.

Při použití kritického tečného napětí

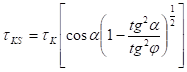
t_KS - kritické tečné napětí na svahu

t_K - kritické tečné napětí na dně.

Posouzení stability pomocí stupně bezpečnosti SF_s

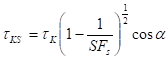     protože

4.8        Stabilita říčního koryta v oblouku

V oblouku říčního tratě nabývá max. svislicová rychlost větší hodnoty než v přímé trati. Zvětšení svislicové rychlosti způsobuje větší vymílání vůči přímé trati. Proto nevymílací rychlost v oblouku musí být menší než v přímé trati, úměrně se zvětšením max. svislicové rychlosti.

Nevymílací průřezová rychlost v oblouku směrodatná pro dno

Nevymílací rychlost na svahu bude ovlivněna sklonem svahu a příčným prouděním. Důsledkem příčného proudění je odchýlení síly F_t o úhel e.

Výsledná síla tření

poměr třecích sil na svahu a na dně bude

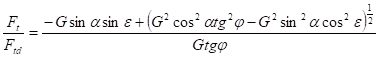
Z poměru třecích sil vyplývá

Protože je uvažován rovnovážný stav bude platit

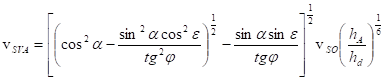
Pro průřezové rychlosti platí

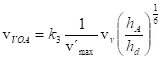
Po dosazení do rovnice pro rovnovážný stav za e jeho střední hodnotu  bude mít rovnice tvar

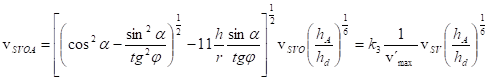
Pro patu svahu

Můžeme předpokládat h_A»h_d pak bude mít rovnice tvar

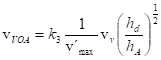
4.9        Deformace říčního koryta

Vytváření výmolů a výskyt nánosů

• je závislé na tvaru rychlostního pole v říčním korytě
• změny v rychlostním poli podmiňují i přetváření příčného profilu koryta
• v přímé trati
• výmol ve střední části koryta
• je-li splněna nerovnost v_smax > v_sv, v > v_v
• v obloucích
• prohloubení v konkávě
• nebude-li proudění ovlivněno rychlostním polem z předcházejícího oblouku, pak vznik výmolu odpovídá velikosti rychlostí v daném oblouku
• platilo-li před obloukem v_smax < v_sv pak v oblouku vznikne výmol v místě kde bude platit v_smax > v_sv a to v důsledku zvětšení v_smax vůči přímé trati.

Délka oblouku bude podmiňovat nejen vytvoření výmolu, ale i jeho umístění. Rozšíření výmolu v konkávě a zvýšené namáhání konkávního břehu způsobuje pak i vznik břehových nátrží.

Usazování splavenin

• v konvexních obloucích
• tam, kde rychlost klesá do té míry, že platí v < v_n, v_s < v_sn.

Výpočet hloubky výmolů

J. Boussinesque

• jeden z nejstarších vztahů pro hloubku výmolů
• vychází z určení hydraulických ztrát v oblouku otevřeného koryta (ztráty třením a ztráty vlivem zakřivení)

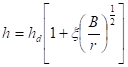
            h_d - hloubka v přímé trati (m)

            B - šířka hladiny (m)

            r - poloměr oblouku (m)

            hodnoty x a C v tabulce 3.12.

Hloubka výmolu d_v = h - h_d   (m)

Max. hloubka výmolu d_vmax = (h-h_d)C           (m)

Velmi jednoduchý vztah uvedla ON 736821. Vztah je stanoven na základě úměrnosti hloubek, průřezových rychlostí v a nevymílacích rychlostí v_v

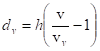
Průřezové rychlosti lze nahradit svislicovými rychlostmi. Pak lze posoudit deformaci v celé šířce daného profilu.