3. Činnost a vývoj přirozených aluviálních toků
I v dnešní době, kdy máme k dispozici velké množství výpočetní techniky a značné znalosti, je třeba se v oblasti hydromechaniky zabývat pouze zjednodušenými a často ze souvislosti vztrženými problémy.
Důležité jsou experimentální modelové výzkumy, pomocí kterých potvrzujeme teoretické hypotézy.
V současnosti již nejsou empirické poznatky o zákonitostech vývoje přirozených vodních toků tím jediným a nejpodstatnějším co nám umožňuje řešit problémy říční hydromechaniky, přesto se bez nich při návrhu úprav neobejdeme.
V úpravách toků se zabýváme především aluviálními toky, tzn. toky v zóně v níž převládá akumulace (toky staré) nebo transport splavenin (toky dospělé). Toky mladými v nichž převládá hloubková eroze se zabývá obor hrazení bystřin.
3.1 Půdorysné tvary a klasifikace aluviálních toků
Přímá koryta
- natvoří vlnovku
- v přírodě vzácná, tok může mít relativně přímé břehy, ale hlavní proudnice (případně spojnice max. rychlostí) je obvykle zakřivená
- pro rozlišení přímého a meandrujícího toku se používá VLNOVITOST-poměr mezi délkou spojnice největších hloubek (úžlabnicí) a délkou údolí (údolnicí), tu lze nahradit přímou vzdáleností. Charakterizuje stupeň zvlnění půdorysného obrazu koryta s nabývá hodnot 1 až 3 a více
- s = 1,5 je hranice mezi meandrujícími a přímými toky naší definici v normě odpovídá hraniční hodnota s = π/2
- úseky toků, které jsou na relativně dlouhé délce přímé jsou většinou považovány za nestabilní, neboť proud přechází nekontrolovaně od jednoho břehu ke druhému
- vznikají:
- přirozeným nebo umělým protnutím šíje meandru, změní se relativně pozvolný podélný sklon a dlouhá délka meandru na kratší úsek s mnohem větším sklonem
- vytvořením prizmatického opevněného koryta
- výstavbou koncentračních staveb
- za nízkého vodního stavu proudnice meandruje jen mezi splaveninovými lavicemi
- za vysokého vodního stavu vznikají krátké oblasti velkých hloubek a relativně dlouhé mělké brodové úseky
- přímé koryto je charakterizováno pohyblivými splaveninovými lavicemi a jejich stabilita determinuje stabilitu úseku.
Rozvětvená koryta
široké, s obtížně definovatelnými břehy. Je charakterizováno strmými a mělkými tratěmi s několikanásobně členěným korytem rozděleným aluviálními ostrovy (středovými splaveninovými lavicemi)
Příčiny, které vyvolávají rozvětvená koryta:
- přesycení proudu splaveninami - tok je zásobován větším množstvím splavenin než je schopen transportovat, část splavenin se ukládá v nánosových útvarech
- strmé sklony šikmých a mělkých koryt - erozní činností se vytvářejí pohyblivé lavice a ostrovy
- oba - tok je přesycen, vznikají nánosy, zvětšuje se podélný sklon dolního úseku. Jakmile se sklon zvětší dostatečně, zvětší se rychlost a vyvíjejí se členěná koryta
- splaveninové lavice vznikají v rozsahu hlavního koryta jsou nestabilní a mění polohu s časem i vodním stavem
- zvláštní příčinou větvení jsou koryta se snadno erodovatelnými břehy. Za vysokých průtoků se vodní tok rozšiřuje, za nízkých průtoků se pohyblivé lavice samovolně stabilizují (náletovou vegetací) a tvoří se ostrovy
- obtížně a náročně se upravují, jsou nestabilní, nesou velké množství splavenin, jsou široké a mělké i při povodňových průtocích
- mají strmý sklon, velký pohyb dnových splavenin, malý obsah jílových částic v materiálu dna a břehů
- výskyt v oblasti s převahou transportu splavenin-podhorské oblasti (usazovaní nejhrubších splavenin).
Meandrující koryta
- skládá se ze střídajících se zákrutů, jejichž tvar nelze převážně definovat kvůli měnícímu se přírodnímu prostředí jímž koryto prochází
- skládá se ze série výmolů v obloucích (tůní) a z mělkých brodů (krátké přímé úseky spojující meandry)
- proudnice přechází z tůně přes brod do následujícího výmolu, vytváří vlnovku
- příčinou meandrování je:
- existence trojrozměrného šroubovitého (příčného) proudění v zákrutu-proudnice osciluje napříč korytem, což je počátek formování oblouků
- eroze břehů
- nerovnoměrné ukládání splavenin vlivem různých singularit (stromy působící překážku v proudu)
- Coriolosova síla
- materiál erodovaný z konkávních břehů se ukládá na nepohyblivé splaveninové lavici, která se vytváří v následném oblouku u téhož břehu, částečně je transportován k protějšímu konvexnímu břehu. Tyto lavice zužují koryto a umožňují pokračování eroze. Proti pevné lavici je eroze největší
- tvar pevné lavice jednoznačně definuje směr proudu, její největší rozměr je orientován směrem po proudu. Narůstají-li lavice směrem po proudu zákrut postupuje dolů. Při rychlé erozi břehů a rychlém postupu meandrů mohou vznikat v oblasti brodů středové lavice až ostrovy
- meandrový pás (je vymezen obalovými čarami meandrujícího koryta) jako celek postupuje po proudu, jednotlivé meandry se pohybují každý jinak-různá erodovatelnost břehů
- šíje meandru se postupně zužuje, až dojde k protnutí a vznikne komunikačně odloučený ostrov. Zkrácením toku se zvýší podélný lokální sklon a začne se vyvíjet nový meandr. Geometrie závisí na lokálním podélném sklonu, materiálu břehů a geometrii sousedních zákrutů. Časem dojde vlivem lokálního strmého sklonu k odstavení i sousedních meandrů.
- než se odstavená ramena naplní sedimenty trvá někdy dlouhé období. V horním konci se usazují hrubší sedimenty (splaveviny) a vytváří se nový břeh. Při rozlivech při povodních se plní jemným materiálem s vodou.
Slepé rameno - dolní konec jezera je spojen s tokem (voda při poklesu povodně tudy odtéká)slepé rameno.
Odstavené rameno - je-li odděleno na obou koncích, ale je zajištěna umělá komunikace s tokem.
Mrtvé rameno - odděleno na obou koncích, ale bez komunikace.
Slepé i ostavené rameno jsou součástí vodního toku, mrtvé už není.
jemné nánosy jílů a siltů usazené v meandrovém pásu údolní nivy jsou plastické a soudržné. Při dalším vývoji protíná tok stará ramena zaplněná těmito zátkami, tyto jsou odolnější vůči erozi a tím mohou výrazně ovlivnit další vývoj geometrie koryta
agradační valy
- charakteristické pro staré říční systémy.
- jsou to přirozené přírodní pobřežní hráze
- z hrubších materiálů, snadněji se usazují při rozlivech do inundačního území
- za nimi vznikají bezodtoková bažinatá území
- jakmile dosáhnou výšky odpovídající průměrnému vodnímu stavu, jejich rychlost růstu se podstatně sníží
3.2 Příčný a podélný profil meandrujících toků
Tvar koryta v brodu:
- obdelník
- trojúhelník - max. hloubka je u konkávního břehu, pevná splaveninová lavice je u konvexního břehu (splaveninová lavice je stálá v čase i umístění, mění pouze velikost a tvar s průtokem) .
Při nízkých vodních stavech jsou:
- v brodech lokální podélné sklony strmější a rychlost větší než ve výmolech
- brod je tvořen splaveninovým útvarem, který při nižších vodních stavech vyvolává vzdutí do předchozího zákrutu, dojde ke zvětšení hloubky
- proudnice se přimyká ke konkávnímu břehu (při vysokém vodním stavu se napřimuje), přes brod však prochází v obou případech v přibližně stejném místě
- oblast brodu je definována i křížením hlavní proudnice s pásem splaveninových útvarů spojujících splaveninové lavice ve dvou sousedních obloucích. (obr 4.4).
Při změnách průtoků dochází ke změnám tvaru a velikosti výmolů a brodů.
Zvětšení průtoků:
- zvětší se intenzita eroze břehů, do pohybu se dává velké množství větších zrn, ty se ukládají v dolní části (u paty) brodu, ten narůstá směrem po vodě (obr. 4.5).
Vysoké vodní stavy:
- podélný sklon hladiny je plynulý a vyrovnaný.
Pokles vodních stavů:
- sníží se podélný sklon a rychlost proudění ve výmolech, zvětší se sklon a rychlost v brodech, splaveniny jsou odplavovány z brodů do dolního výmolu, sníží se vrchol brodu a dojde ke zdánlivému posunu vrcholu brodu proti vodě.
- dolní výmol se zaplňuje a tok se snaží vytvořit vyrovnaný podélný profil.
- nejhrubší splaveniny odolávají a dále se zvýrazňuje rozdíl v charakteru proudu v brodech a ve výmolech.
- může dojít až k extrému, kdy proudění v brodech má až charakter bystřinného proudění s vodním skokem při přechodu do dalšího oblouku.
U dostatečně vyvinutých meandrů se stává, že výmoly u jednoho břehu zasahují až pod začátek výmolu v následujícím oblouku u protějšího břehu (obr. 4.6). Brod je ve tvaru úzkého, vysokého a strmého splaveninového útvaru ve formě prahu. Je labilní, reaguje změnou polohy i velikosti na změnu vodního stavu. Jedná se o tzv. „špatný brod“ (bráno z hlediska překonávání vodního toku).
3.3 Vzájemná souvislost typů aluviálních koryt
Za nejstabilnější je považováno meandrující koryto se stabilními oblastmi výmolů a s pevnými splaveninovými lavicemi. Skutečná koryta nemohou nikdy dospět k rovnovážnému stavu z těchto důvodů:
- nestacionarita průtoků
- nehomogenita vlastností materiálu koryta
- cyklická změna vegetace na březích a v korytě.
Lze však pozorovat u přirozených říčních úseků určité zákonitosti mezi :
- břehovým průtokem-průtok odpovídající přirozené kapacitě koryta
- proudovými charakteristikami
- geometrickými charakteristikami tvaru koryta-půdorysného obrazu i tvaru příčných profilů
- vlastnostmi materiálu koryta-charakterizovanými zrnitostním složením.
Jsou-li uvedené parametry v dostatečně těsném statistickém vztahu, můžeme vodní tok považovat za tok v režimu.
Dojde-li k přirozené, nebo umělé změně sklonu koryta (např. odstavení meandru), změní se režim toku a následně i půdorysný tvar koryta-např. z meandrujícího na rozvětvený, případně naopak i slabé zmenšení podélného sklonu může změnit nestabilní rozvětvený tok na stabilnější meandrující (obr. 4.7).
Podle E. W. Laneho platí vztah mezi sklonem, průtokem a typem koryta.
Rovnice
![]()
charakterizuje toky s pískovým dnem s tendencí meandrovat.
Platí-li
![]()
tok se větví na ramena. V rozmezí obou hodnot je oblast přechodná do níž patří také většina toků u nás.
3.4 Určení odezvy toku na změny v režimu
Pro určení kvantitativní odezvy obvykle nejsou dostatečné podklady, provádí se tedy pouze kvalitativní odhad.
Ze studií pánů Laneho, Leopolda, Maddocka, Schumma, Santose ad. vyplývají závislosti:
h ~ Q h - hloubka vody
B ~ Q Q - průtok vody
~Qs Qs - průtok splavenin
B/h ~ Qs B/h - poměr šířky a hloubky, vyjadřuje tvar příčného profilu
i ~ Q i - podélný sklon koryta
~ Qs
~ d50 d50 - velikost průměr. zrna
s ~ sklon údolí s - vlnovitost
~ Qs
Qs ~ (t0.v) t0.v - výkon proudu na jednotku plochy dna (W.m-2)
~ CF CF - koncentrace jemných částic
~ d50
![]()
zavedeme-li ![]()
![]()
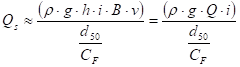
Předpokládáme r.g = konst, CF zahrneme v zrnitostním složení splavenin a vyjádříme ji tím v d50. Pak je vztah zjednodušen na
![]()
Uvedené vztahy jsou nejvíce používané pro prognózu odezvy koryta na zásahy do říčního systému.
Př. Máme malý přítok s velkým množstvím splavenin. Qs se zvětší na Qs+, sklon i pod bodem C se zvětší pokud Q a d=konst. CA se posune do CA´. Horní úsek nad soutokem se za dlouhé časové období vyrovná do původního sklonu.
3.5 Vzájemné vztahy geomorfologických a hydraulických charakteristik toku
Nejlépe se znázorňují graficky.
znázornění proudnic při vysokém a nízkém vodním stavu
nízký stav - proudnice sleduje vnější konkávní břeh meandru, na relativně velké délce přechází do dalšího meandru
vysoký stav-proudnice zkracuje dráhu, protéká oblast stabilní splaveninové lavice u vnitřního břehu
redukce délky při vysokém vodním stavu vyvolá zvýšení sklonu v zákrutu (stejný vliv jako zkrácení toku).
-při úpravě je nutné navrhnout vlnovitost (zakřivení oblouků) při nízkém vodním stavu tak velkou, aby zabezpečila, že při vysokém vodním stavu a tomu odpovídajícímu zvýšení sklonu nebude mít tok tendenci přejít na rozvětvený.
-limitní sklon zjistíme z obrázku
vyjde-li pro daný úsek pro vysoký vodní stav přechod do středního pásma, návrh je přijatelný, ale hrozí nebezpečí snadného přechodu do oblasti rozvětvení.
režim aluviálního toku je v úzkém vztahu k výkonu na jednotku plochy t0.v a odpory proudu pro dané zrnitostní složení d50
t0.v a d50 - jsou funkcí typu dnových útvarů
při nízkém vodním stavu
-dnové útvary odpovídají dolnímu režimu
-tvarový odpor výrazně zvětšuje celkové odpory proudu
-při vysokém vodním stavu
-režim přechází do hlavní tranzitní zóny
-odpory se zmenšují a tím ovlivňují zdánlivý pokles snížení vodního stavu
znázorňuje přímý vliv změny režimu na odpory.
znázorněna normální křivka Q=f(h) s konstantními odpory proudu.
je popsán schematický návod na postup u konkrétního toku
skutečná schémata je nutno odvodit z dat získaných z říčního systému
následně pak jen pro daný tok mohou být tato schémata aplikována.
3.6 Fargeuovy teze vývoje přirozeného říčního toku
L. Fargue sledoval přeměny koryta na řece Garonne. Sledoval a srovnával příčné profily a zakřivení oblouků. Došel k závěru, že změna půdorysného obrazu trasy toku způsobuje i změnu příčného profilu toku.
Vyvodil závěry:
1. Max. hloubky jsou v bodě obratu mezi dvěma protisměrnými oblouky.
2. Max. hloubky odpovídají vrcholu oblouku. Vrchol oblouku je ta část, která má max. zakřivení. Křivost r = 1/R.
3. Max. hloubka je tím větší, čím je zakřivení vrcholu oblouku výraznější.
Postupným shrnováním poznatků přepracoval své závěry do následujících:
Výskyt maximálních a minimálních hloubek
- Extrémy oblouků (max. a min. křivost) neleží na stejných pořadnicích s extrémy koryta (max. a min. hloubka vody).
- Oblouky mění polohu a konvexní břehy se posunují směrem po proudu.
Nejmenší hloubky
vznikají v určité vzdálenosti po proudu od místa nejm. křivosti (inflexní bod, brod).
poměr vzdálenosti min. hloubky od extrému oblouku a délky oblouku je tzv. součinitel odchýlení. Prům. hodnota 0,25.
Maximální hloubky
každému vrcholu oblouku náleží max. hloubka daného okolí odchýlená od vrcholu po proudu.
odchýlení je zhruba stejné jako odchýlení nejm. hloubky od obratu oblouků.
Teze největších hloubek
- Max. hloubka za vrcholem oblouku je tím větší, čím je křivost jeho oblouku výraznější.
- odvodil empirický vztah:
r=1/R=0,03hmax3-0,23hmax2+0,78hmax-0,76
R - poloměr (km), hmax - max. hloubka v oblouku (m).
- vztah přestává platit, jestliže se délka konkávního oblouku výrazně odlišuje od stř. délky oblouku.
Teze úhlu
- Vyjadřuje závislost stř. hloubek koryta na změně stř. křivosti příslušného oblouku.
- průměrná hloubka v oblouku s délkou 1 je výjadřena stř. hodnotou integrálu:
h=1/l ò hds
- stř. hodnota křivosti oblouku:
r=1/l ò rds=1/l ò 1/R.R.da
- ze závislosti r a h vyplývá, že vzrůst r je závislý na délce
oblouku a tedy i úhlu a, zároveň se zvětšují průměrné hloubky . Na základě tohoto poznatku vyslovuje
Teze úhlu oblouku
- Při vzrůstu vnějšího úhlu tečen daného oblouku se zvětší i průměrné hloubky.
Teze vývoje
- Při průměrné délce oblouků ze všech zkoumaných oblouků je hloubka toku největší.
- nejvýhodnější délka oblouku je ta, která se rovná průměrné délce.
Teze sklonu
- Sklon dna koryta je určen sklonem tangenty ke křivce křivosti.
- vystihuje závislost mezi změnou křivosti, změnou hloubek, sklonem dna.
- podle změn křivosti se dělí křivky průběhu křivosti na:
a) křivky spojité
b) křivky konstantní křivosti
c) křivky nespojité
- b), c) - náhlá změna křivosti odpovídá náhlé změně hloubek.
- a) - čára vyjadřující průběh dna v místech největších hloubek vykazuje odpovídající pravidelnosti jako křivka křivosti.
Průměrná křivost r = 106Dr/Dh
Průměrná hloubka h = 103Dh/Dl
Fargueovy doporučení pro úpravu toku:
a) šířka koryta v bodech obratu < šířka koryta v oblouku.
b) zúžení koryta může nahradit vhodné rozdělení křivosti oblouků.
c) křivka křivostí i křivka hloubek jsou sinusoidy.
d) konkávní břeh osciluje kolem křivky odpovídající kruhovému oblouku.
e) oblouky říčních koryt se blíží tvaru lemniskátových oblouků.
Fargueovy závěry znamenaly první formulaci zákonitostí vývoje přiroz. říčních toků. V technické praxi se uplatňují dodnes. Nemají zcela obecnou platnost. Byly odvozeny pro koryto s jemnozrnými splaveninami.
3.7 Leljavského metoda
- vyšel ze snahy o zajištění dostatečné průběžné hloubky pro plavbu
- všímá si přeměn říčního koryta a odtud zjišťuje:
- u konkávních břehů dochází k erozi dna
- erodovaný materiál je unášen do konvexy, kde sedimentuje
- proudnice nejsou rovnoběžné s břehy, mění směr od jednoho břehu ke druhému
- existence příčného proudění a jeho přetvárnou práci na tvaru říčního koryta.
Na základě těchto poznatků upouští od Fargeuova doporučení použití sinusoid. obloku a doporučuje zvětšení křivosti v konci oblouku před přímou tratí a při napojení na druhý protisměrný oblouk.
Výsledkem je prodloužení tratě s většími hloubkami, než v běžném brodovém úseku a dosažení napojení na konkávu dalšího oblouku při zvětšených hloubkách.
Fargeuově tezi o náhlé změně hloubek v souvislosti s náhlou změnou křivosti odporují výsledky experimentů různých autorů:
Výbora: experiment s modelem říčního koryta s pohyblivým dnem. Modeloval říční trať složenou z kruhového a lemniskátového oblouku o středovém úhlu 90°s připojenými přímými úseky.
Výsledky:
- výmol se tvoří v závislosti na vývoji příčného proudění a max. hloubky, v místech max. stř. svislicových rychlostí.
- výmol se prodloužil za oblouk
- začátek oblouku měl stejný tvar jako přímá trať
- lze tedy při úpravách použít i kruhový oblouk
Výsledky dalších experimentů: při krátkých obloucích (do 45° středového oblouku), kdy max. stř. svislicová rychlost zůstává ve střední třetině lze tyto napojit přímo na sebe, výmol zůstává v ose koryta.
3.8 Fyzikální modelování
- někdy je nutný trojrozměrný model
- simulují vliv jezů, mostů, odběrů, výpustí, zaústění
- při předpovídání povodně - rozsah, charakter proudění
- podmínkou je znát potřebné parametry - průtoky, zrnitost materiálu dna, geometrický tvar, průběh hladin
- používá se Froudovo kritérium podobnosti
Fr=v/(g.l)1/2
- musí platit Frmodelu=Frskutečné
